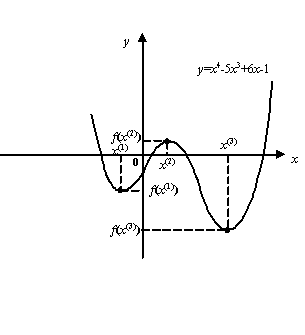
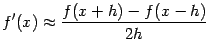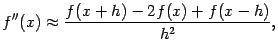Как уже отмечалось выше, если известно, что точка локального экстремума
функции ![]() на отрезке
на отрезке
![]() единственна и лежит внутри отрезка, то в
этой точке
единственна и лежит внутри отрезка, то в
этой точке ![]() выполняется равенство
выполняется равенство ![]() . Таким
образом, для нахождения точки локального минимума с точностью
. Таким
образом, для нахождения точки локального минимума с точностью ![]() нужно с
этой точностью найти корень уравнения
нужно с
этой точностью найти корень уравнения ![]() . Будем предполагать, что для функции
. Будем предполагать, что для функции ![]() известно аналитическое выражение или мы умеем вычислять
значения
известно аналитическое выражение или мы умеем вычислять
значения ![]() при
заданном
при
заданном ![]() каким-либо иным способом. Для нахождения
корня мы можем применить один из приближённых методов решения уравнений, которые
мы обсуждали в этой главе ранее.
каким-либо иным способом. Для нахождения
корня мы можем применить один из приближённых методов решения уравнений, которые
мы обсуждали в этой главе ранее.
Например, метод Ньютона, применённый к уравнению ![]() , даёт итерационную формулу (см. формулу (9.1)):
, даёт итерационную формулу (см. формулу (9.1)):
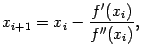
Метод хорд даёт итерационную формулу (см. формулу (9.3)):
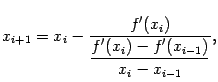
Эти методы весьма эффективны, если выполняются условия их применимости. Их достоинства и недостатки -- продолжение тех же свойств соответствующих методов приближённого поиска корня.
Осталось найти точки ![]() и
и ![]() , вычислить в них значения функции и
сравнить эти значения.
, вычислить в них значения функции и
сравнить эти значения.
Точки ![]() будем
искать как корни уравнения
будем
искать как корни уравнения ![]() , применяя
метод Ньютона. Поскольку
, применяя
метод Ньютона. Поскольку ![]() , то
итерационная формула метода Ньютона для поиска любой из трёх точек
, то
итерационная формула метода Ньютона для поиска любой из трёх точек ![]() будет иметь вид
будет иметь вид
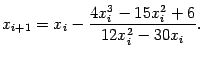
Точка ![]() отделена
на отрезке
отделена
на отрезке ![]() , значит,
возьмём за начальное приближение
, значит,
возьмём за начальное приближение ![]() . Далее,
применяя итерационную формулу, получаем (с точностью
. Далее,
применяя итерационную формулу, получаем (с точностью ![]() ):
):
Беря за начальное приближение ![]() , получаем
последовательные приближения к
, получаем
последовательные приближения к ![]() :
:
Теперь возьмём за начальное приближение для ![]() значение
значение ![]() . Получаем
последовательные приближения
. Получаем
последовательные приближения
Сравнивая два значения в точках локального минимума, получаем, что